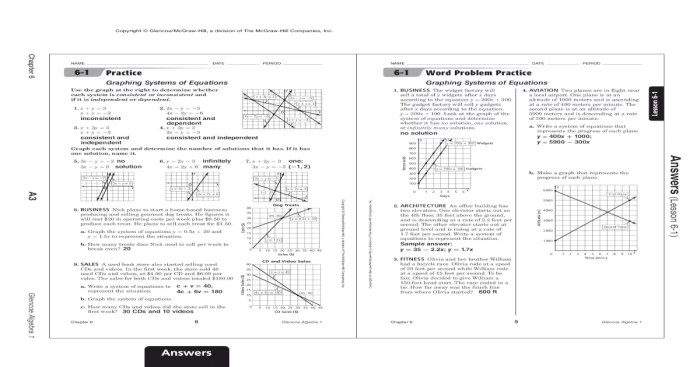
Introducing the Solve Equations with Variables on Both Sides Worksheet, a meticulously crafted resource designed to empower students with the skills to conquer algebraic equations. This comprehensive guide provides a structured approach, clear instructions, and diverse problem types to foster a deep understanding of variable isolation techniques and solution verification.
Delving into the intricacies of algebraic equations, this worksheet equips students with the ability to isolate variables, maintain equation balance, and apply multiple techniques to solve complex problems. With a focus on accuracy and higher-level thinking, the Solve Equations with Variables on Both Sides Worksheet empowers students to tackle algebraic challenges with confidence.
Worksheet Design
An effective worksheet layout provides a structured and organized environment for students to solve equations. It should include clear instructions, examples, and step-by-step guides to facilitate understanding and successful completion of the tasks.
Create a Structured Worksheet Layout
- Establish a logical flow of equations, starting with simpler ones and gradually increasing complexity.
- Provide ample space for students to work out their solutions, ensuring they have enough room to show their steps clearly.
- Include a designated area for students to write their final answers, promoting clarity and organization.
Provide Clear Instructions for Solving Equations
- Explain the steps involved in solving equations, including isolating variables and performing mathematical operations.
- Provide specific examples to illustrate the process, ensuring students understand the concepts before attempting the exercises.
- Emphasize the importance of checking solutions to verify accuracy, encouraging students to substitute their answers back into the original equations.
Include Examples and Step-by-Step Guides, Solve equations with variables on both sides worksheet
- Incorporate worked-out examples to demonstrate the application of the techniques taught.
- Provide step-by-step guides that break down complex equations into manageable steps, making the process more accessible to students.
- Offer hints or suggestions to assist students who may encounter difficulties, promoting problem-solving skills.
Variable Isolation Techniques
Isolating variables on one side of an equation is crucial for solving it. Various techniques can be employed to achieve this, each with its own advantages and applications.
Explain Methods for Isolating Variables on One Side
- Addition and Subtraction: Adding or subtracting the same value to both sides of an equation maintains equality while isolating the variable on one side.
- Multiplication and Division: Multiplying or dividing both sides of an equation by the same non-zero value isolates the variable on one side, provided the value is not zero.
- Combining Like Terms: When variables and constants appear on both sides of an equation, combining like terms simplifies the equation, making it easier to isolate the variable.
Provide Examples of Using Addition, Subtraction, Multiplication, and Division
- Addition: 2x + 5 = 11; add
-5 to both sides
2x = 6
- Subtraction: 3y
7 = 15; subtract 15 from both sides
3y = 22
- Multiplication: (1/2)z = 10; multiply both sides by 2: z = 20
- Division: 4w / 8 = 5; divide both sides by 4: w = 10
Discuss the Importance of Maintaining Equation Balance
It is essential to maintain the balance of an equation throughout the solving process. Any operation performed on one side of the equation must also be performed on the other side to preserve equality. Failure to do so will result in an incorrect solution.
Problem Types and Examples: Solve Equations With Variables On Both Sides Worksheet

Equations with variables on both sides can vary in complexity and type. Understanding the different types and their corresponding techniques is crucial for successful problem-solving.
Present a Variety of Equation Types with Variables on Both Sides
- One-Step Equations: x + 5 = 10
- Two-Step Equations: 2x- 7 = 11
- Multi-Step Equations: 3(x + 2) = 2x- 5
- Equations with Fractions: (1/2)y + 3 = 7
- Equations with Decimals: 0.5x- 1.2 = 2.3
- Equations with Exponents: 2^x = 16
Provide Multiple Examples for Each Type
- One-Step Equations: x
3 = 7; x + 10 = 15
- Two-Step Equations: 2y + 5 = 13; 3z
8 = 14
- Multi-Step Equations: 4(x
- 1) = 2x + 6; 5(2y + 3) = 3(y
- 1)
- Equations with Fractions: (1/3)x + 2 = 5; (3/4)y
1 = 6
- Equations with Decimals: 0.25x + 0.5 = 1.25; 0.75y
0.25 = 1.5
- Equations with Exponents: 3^x = 27; 2^(x
1) = 8
Solution Verification

Verifying solutions is a crucial step in the equation-solving process, ensuring accuracy and building confidence in the results obtained.
Guide Students on Checking Their Solutions
- Substitute the solution back into the original equation.
- Evaluate both sides of the equation to check if they are equal.
- If both sides are equal, the solution is correct.
- If both sides are not equal, the solution is incorrect and the equation-solving process should be reviewed.
Explain the Process of Substituting Values Back into the Original Equation
To verify a solution, substitute the value of the variable obtained into the original equation. Replace the variable with its solution and perform the necessary calculations.
Emphasize the Importance of Verifying Accuracy
Verifying solutions is essential to ensure that the answer obtained is correct. It helps students identify errors in their work and reinforces the concept of equation balance.
Challenge Problems
Incorporating challenging problems into a worksheet encourages students to apply their understanding of equation-solving techniques to more complex scenarios.
Design Challenging Equations that Require Higher-Level Thinking
- Incorporate equations with multiple variables, requiring students to solve for more than one unknown.
- Include equations with non-integer coefficients or exponents, testing students’ ability to handle more complex operations.
- Design equations that require students to combine multiple techniques, such as isolating variables, combining like terms, and using algebraic properties.
Encourage Students to Apply Multiple Techniques
Challenge problems should encourage students to draw upon their knowledge of various equation-solving techniques and apply them creatively to find solutions.
Provide Hints or Guidance for Complex Problems
For particularly complex problems, provide hints or guidance to assist students in their problem-solving process, without giving away the solution.
Worksheet Evaluation
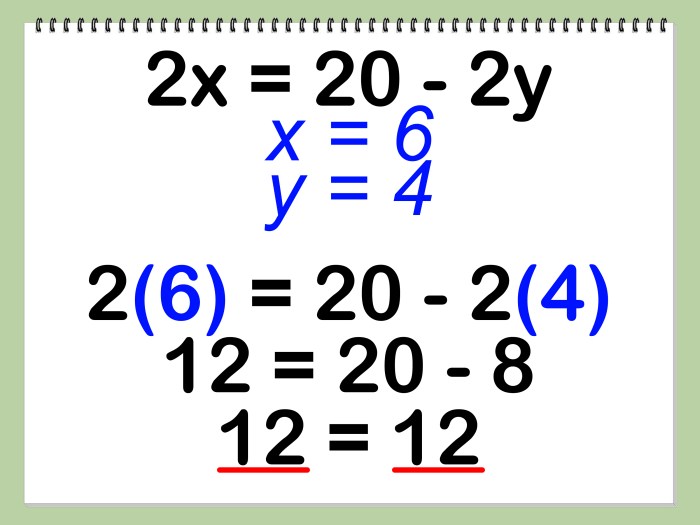
A well-designed worksheet evaluation system provides students with clear feedback on their performance and helps educators assess their understanding of equation-solving concepts.
Provide Clear Grading Criteria
- Establish clear criteria for evaluating students’ work, including accuracy, completeness, and problem-solving strategies.
- Communicate the grading criteria to students before they begin working on the worksheet.
- Use a rubric or scoring guide to ensure consistent and objective evaluation.
Include Answer Keys or Solution Sheets
Provide answer keys or solution sheets to students to facilitate self-assessment and allow them to check their work.
Consider Using a Scoring Rubric to Assess Understanding
A scoring rubric can help educators assess students’ understanding of equation-solving concepts by evaluating their ability to:
- Isolate variables
- Perform algebraic operations
- Verify solutions
- Solve multi-step equations
FAQ Compilation
What are the benefits of using the Solve Equations with Variables on Both Sides Worksheet?
The worksheet provides a structured approach, clear instructions, and diverse problem types to enhance understanding of variable isolation techniques and solution verification.
How does the worksheet help students isolate variables?
The worksheet explains methods for isolating variables on one side using addition, subtraction, multiplication, and division, emphasizing the importance of maintaining equation balance.
What types of equations are covered in the worksheet?
The worksheet presents a variety of equation types with variables on both sides, including equations with fractions, decimals, and exponents, providing multiple examples for each type.