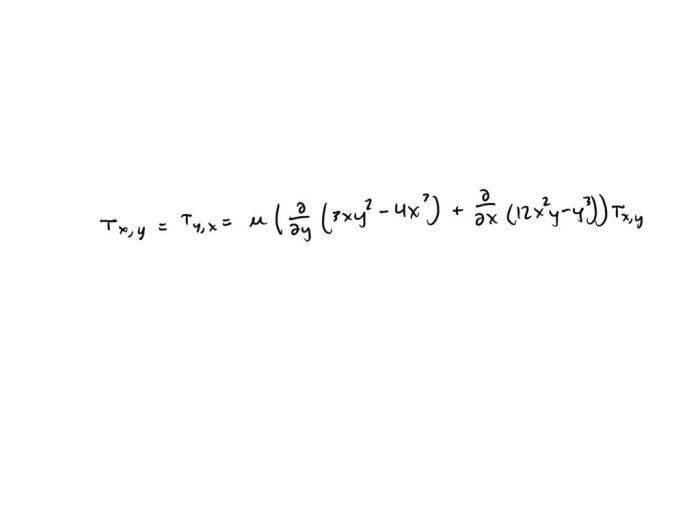Determine the shearing stress for an incompressible newtonian fluid – Shearing stress plays a crucial role in the behavior of fluids, and its determination is essential in various engineering and industrial applications. This article explores the concept of shearing stress in incompressible Newtonian fluids, deriving the mathematical equation and discussing experimental methods for its determination.
By understanding the significance of shearing stress, engineers can optimize fluid systems and processes, leading to improved performance and efficiency.
Incompressible Newtonian fluids exhibit a linear relationship between shear stress and velocity gradient, making them a fundamental model for fluid mechanics. This article provides a comprehensive overview of shearing stress determination in incompressible Newtonian fluids, covering both theoretical and practical aspects.
Introduction
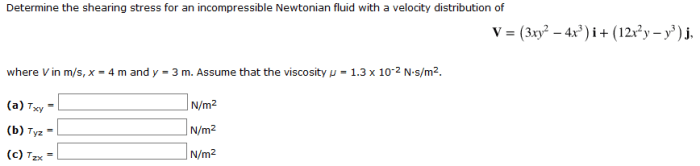
Shearing stress is a fundamental concept in fluid mechanics that describes the force per unit area acting on a fluid due to the relative motion of adjacent layers. In an incompressible Newtonian fluid, the shearing stress is directly proportional to the velocity gradient.
This relationship is known as Newton’s law of viscosity.
Shearing stress plays a crucial role in various engineering and industrial applications, such as the flow of fluids in pipes, the operation of pumps and turbines, and the design of aircraft wings.
Mathematical Formulation
For an incompressible Newtonian fluid, the shearing stress (τ) is given by:
τ = μ
du/dy
where:
- μ is the dynamic viscosity of the fluid
- du/dy is the velocity gradient in the y-direction
This equation highlights the direct proportionality between shearing stress and velocity gradient.
Experimental Determination, Determine the shearing stress for an incompressible newtonian fluid
Shearing stress can be experimentally determined using viscometers, which are devices designed to measure the viscosity of fluids. Common types of viscometers include:
- Capillary viscometers
- Rotational viscometers
- Falling ball viscometers
These viscometers operate on different principles but share the common goal of measuring the resistance of a fluid to flow, which is directly related to the shearing stress.
Applications
Shearing stress has numerous applications in engineering and industrial processes:
- Fluid flow in pipes:Shearing stress is a key factor in determining the pressure drop and flow rate in pipelines.
- Pump and turbine design:The efficiency of pumps and turbines depends on the shearing stress generated within the fluid.
- Aircraft wing design:The aerodynamic forces acting on an aircraft wing are influenced by the shearing stress in the surrounding air.
Understanding and manipulating shearing stress is essential for optimizing the performance of these systems.
Limitations and Considerations
The incompressible Newtonian fluid model has limitations:
- Incompressibility:It assumes the fluid density remains constant, which may not be valid for highly compressible fluids.
- Newtonian behavior:It assumes the fluid’s viscosity is constant, which is not true for non-Newtonian fluids.
In such cases, more complex models and experimental techniques are required to accurately characterize the fluid’s behavior.
Q&A: Determine The Shearing Stress For An Incompressible Newtonian Fluid
What is the significance of viscosity in determining shearing stress?
Viscosity is a fluid property that represents its resistance to flow. It plays a crucial role in determining shearing stress, as fluids with higher viscosity exhibit greater resistance to shear forces.
How can experimental methods be used to determine shearing stress?
Experimental methods, such as viscometers, can be employed to measure shearing stress directly. These devices apply controlled shear forces to a fluid sample and measure the resulting deformation or flow rate.
What are the limitations of the incompressible Newtonian fluid model?
The incompressible Newtonian fluid model assumes constant density and linear stress-strain behavior. However, in certain applications, fluids may exhibit non-Newtonian behavior or compressibility effects, which require more complex models.